Wszyscy pamiętamy teleturniej "Idź na całość", lecący jeszcze niedawno w polskiej telewizji. W końcowej fazie konkursu, gracz wybierał jedną z trzech bramek, licząc na to, że właśnie pod wybraną znajdzie się samochód. Z konkursem tym wiąże się ciekawa matematyczna zagadka, którą postaram się przedstawić w tym temacie.
Monty Hall, urodzony 25 sierpnia 1921 roku, kanadyjski aktor i piosenkarz, gospodarz popularnych programów telewizyjnych. Od jego nazwiska pochodzi znany w rachunku prawdopodobieństwa paradoks Monty Halla. Każdy z nas spotkał się z tym paradoksem oglądając chociażby teleturniej "Idź na całość."
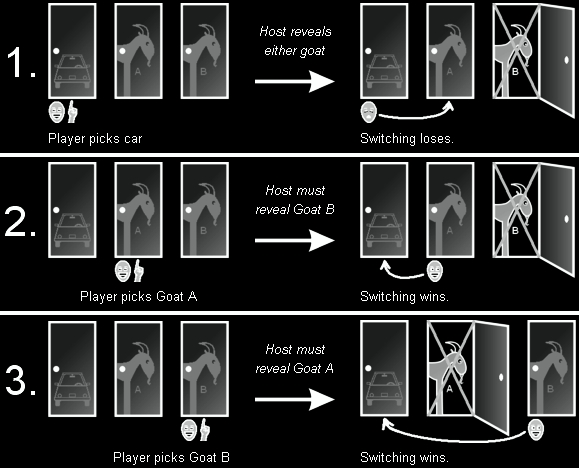
Wszyscy pamiętamy przebieg rozgrywki. Gracz wybiera jedną z trzech bramek. Bramkę nr. 1, nr. 2 lub nr. 3. Następnie prowadzący otwiera jedną z bramek, które nie zostały wybrane i ukazuje nagrodę niższej rangi. Na placu gry pozostają dwie bramki. Wybrana przez gracza i ta nieodsłonięta. Pytanie brzmi: czy gracz powinien zmienić swój wybór, czy raczej pozostać przy wyborze pierwotnym? Jakie znaczenie ma zmiana decyzji?
Innymi słowy, jeśli gracz wybrał bramkę nr 1, a prowadzący odsłonił zawartość bramki nr 2 ukazując "zonka" (czyli przegraną), to czy nowy samochód kryje się za bramką nr. 1 czy raczej za bramką nr. 3?
W tym miejscu, górę biorą neurony i sposób ludzkiego pojmowania. Mózg informuje bowiem, że skoro jedna z bramek została otwarta, to szanse na to, że nagroda kryje się w jednej z pozostałych dwóch, wynoszą 50% czyli inaczej pół na pół. Jednak prawda jest inna. Zostało matematycznie dowiedzione, że jeśli gracz dokona zmiany wyboru z bramki nr 1. na bramkę nr 3. (zgodnie z powyższym przykładem), jego szanse na wygraną wzrosną dwukrotnie.
Jak to możliwe? Nie jest to intuicyjne, ale poprawne. Wielcy matematycy głowili się nad tym problemem przez długi czas. Rozwiązanie jest znane dzisiaj.
Rozpatrzmy problem od strony matematycznej
Wyobraźmy sobie trzy teleturniejowe bramki i gracza, który wybiera jedną z nich. W tym momencie dzieli on bramki na dwa zestawy.
Zestaw A) wybrana bramka
Zestaw B) bramki, które nie zostały wybrane
W tym miejscu, każda z bramek posiada indywidualną szansę na zwycięstwo równą 1 do 3, lub 33%. Biorąc jednak pod uwagę istnienie zestawów A i B, szanse te wyglądają nieco inaczej. Zestaw A jest zestawem zwycięskim z prawdopodobieństwem 1/3. Zestaw B natomiast posiada dwie bramki, a zatem prawdopodobieństwo, że to właśnie B zawiera zwycięską bramkę wynosi 2/3
Zestaw A) - szansa na zwycięstwo = 1/3
Zestaw B) - szansa na zwycięstwo = 2/3
Kiedy prowadzący odsłania jedną z bramek - w zestawie B - ukazując, że jedna z nich nie jest zwycięska, zestaw B wciąż z prawdopodobieństwem równym 2 do 3 jest w naszym schemacie zestawem najlepszym, podczas gdy szansa na zwycięstwo w zestawie A wciąż wynosi tylko 1 do 3. Odsłaniając zawartość jednej z bramek w zestawie B, szanse na to, że druga z nich zawiera nagrodę główną są większe niż początkowy wybór gracza - bramka z zestawu A.
Aby lepiej zobrazować ten przykład, rozszerzmy skalę z 3 do 100 bramek. Gracz wybiera jedną z bramek, a prowadzący odsłania 98 pozostałych, które nie zawierają nagrody. Która z dwóch pozostałych w grze bramek ma większe szanse na zwycięstwo? Ta, wybrana przez gracza na samym początku, gdy wybierał on spośród 100, czy ta, która nie została otwarta spośród 99, których nie wybrał? Odpowiedź jest tylko jedna: szanse na to, że nagroda główna znajduje się w bramce wybranej na początku wynoszą 1 do 100, podczas gdy szansa na to, że nagroda znajduje się w drugiej z nieotwartych bramek wynosi 99 do 100, a zatem jest nieporównywalnie większa.
Podsumowując, zmiana decyzji gracza w powyższych przykładach przynosi mu większą szansę na wygraną, nawet gdy mamy do czynienia z 3 bramkami.
Problem z tą zagadką leży w sposobie rozumowania człowieka. Nasz mózg wyszukuje schematów, odrzucając większość nieschematycznych danych. Taki system działania zwykle sprawdza się doskonale, ponieważ pozwala odrzucać większą część niepotrzebnych informacji, które tylko zbędnie obciążałyby umysł. Czasem jednak potrzeba logicznego myślenia jest konieczna.
Istnieje jeszcze jeden przykład, na zbyt schematyczne myślenie człowieka. Wyobraźmy sobie sytuację, w której podrzucamy monetą 99 razy i za każdym razem otrzymujemy orła. Jakie są szanse na to, że przy kolejnym setnym rzucie, znów wypadnie orzeł? Większość z nas odpowie, że jest to praktycznie niemożliwe, a jednak z matematycznego punktu widzenia szanse te wynoszą 50%.
Powód, dla którego uważamy, że orzeł nie ma prawa wypaść po raz setny z rzędu, związany jest z prawdopodobieństwem takiego scenariusza. Szanse na to, że na 100 rzutów, 100-krotnie uzyskamy orła wynoszą jak 1 do 1,267,650,600,228,229,401,496,703,205,376. Jednakże, jeśli rozpiszemy dowolną sekwencję orłów i reszek dla 100 rzutów, okaże się, że szanse jej uzyskania są równie małe jak uzyskanie serii tych samych rezultatów...
Autor Eurycide
www.paranormalne.pl
oparto o paradoks Monty Halla
inspiracje: damninteresting.com













